Sincronizzazione

Lezione del 2019-05-08 mer.

Concetti base

I processi hanno la necessità di sincronizzarsi. La sincronizzazione può essere necessaria per i segenti motivi:

• concordare rigaurdo l’accesso esclusivo ad una risorsa;

• concordare riguardo l’ordine degli eventi in corso.

La sincronizzazione in un singolo sistema centralizzato è facile da ottenere. Ma quando si ha a che fare con più sistemi autonomi, può essere un requisito molto difficile da perseguire.

In alcuni casi un gruppo di processi ha necessità di concordare un coordinatore (leader).

Consideriamo il problema dell’ordinamento di eventi tra sistemi autonomi, che è alla base anche della gestione dell’accesso a risorse condivise tra sistemi distribuiti.

Il concetto di ordinare eventi è relazionabile al concetto di tempo. Possiamo associare agli eventi una coordinata temporale, e ordinarli secondo il valore di questa coordinata. Ad esempio. Supponiamo vi sia un general clock valido per tutti i processi. Il processo A rileva il tempo dal clock ottenendo t(A). Dopo di che fa la stessa cosa il processo *B, ottenendo t(B). Varrà t(A) <= t(B), e possiamo affermare che l’evento del processo A avviene prima dell’evento del processo B.

Però l’uso di una coordinata temporale non semplifica il problema. Anche questa è semplice da gestire in un sistema centralizzato, ma non lo è in un sistema distribuito. Per capire questo concetto osserviamo il seguente diagramma temporale.

Questo diagramma illustra una possibile situazione anomala che si può creare in un sistema formato da due computer: uno (il superiore) demandato alla compilazione del programma out.c in out.o, e l’altro (coordinata centrale) in cui si effettua l’editing di out.c. Un programma make 1 che confronti l’ora di creazione di out.o (le 2020, secondo il clock locale del computer di compilazione) lo troverebbe successivo all’orario di modifica di out.c (le 2010, secondo il clock locale del computer di editing). In queste condizioni make non ricompila out.o. Invece, usando la coordinata in basso, (che ci mostra il general clock, ovvero il tempo oggettivo) possiamo osservare che out.o è stato creato alle 2010, precedente alle 2020 che è l’orario di editing di out.c. Un make in grado di valutare gli eventi secondo il general clock ricompilerebbe correttamente out.o.

Questo problema è generale. Ad esempio si supponga di voler monitorare un ponte, tramite sensori che inviano i dati a diversi computer. Per confrontare i dati ricevuti da computer diversi, è necessario che i clock locali dei due computer siano confrontabili. Non solo. Se voglio sapere a che ora è accaduto un evento di particolare interesse (ad es. una sollecitazione sismica), devo avere sincronizzazione con un orario valido in generale.

Analogamente se vogliano controllare il movimento di un robot, con sensori di posizione e movimento che inviano i relativi dati a computer diversi. Anche in questo caso, dovendo confrontare i dati collezionati da computer diversi, è necessario sincronizzare i relativi clock.

Non tutti i problemi di sincronizzazione sono uguali. In un determinato contesto è possibile sia sufficiente determinare se un evento è avvenuto prima o dopo un altro evento. In questi casi «basta» avere una temporizzazione logica (si veda oltre). Nell’esempio precedente sarebbe sufficiente sapere se la generazione di out.o è avvenuta prima o dopo la modifica di out.c. Ma vi sono casi in cui questo non basta. Supponiamo di poter accedere ad una risorsa solo in un determinato intervallo temporale. In questo caso è necessario che il computer che richiede l’accesso sia sincronizzato con il clock del controllore secondo la misura fisica del tempo.

Il problema della sincronizzazione dei clock

Quindi: come si possono sincronizzare i clock di computer diversi?

Generalità

Il clock locale di un computer viene usualmente realizzato utilizzando cristalli di quarzo fatti oscillare a determinate frequenza. La frequenza di oscillazione del quarzo dipende, in modo molto sensibile, dalla tensione applicata al suo circuito.

Al quarzo sono associati un contatore a una cella di inizializzazione (holding register). Ad ogni oscillazione del quarzo, il contatore decrementa di uno. Quando arriva a zero viene generato un interrupt e il contatore viene ricaricato con il contenuto del registro di inizializzazione. L’interrupt viene ricevuto dal sistema operativo, che aggiorna di conseguenza il proprio contatore temporale (ovvero il clock fisico del computer).

La sincronizzazione del tempo fisico richiede la sincronizzazione dei clock delle cpu coinvolte nel sistema distribuito.

Garantire che la frequenza di oscillazione dei cristalli che pilotano i diversi clock sia uguale per tutti è impossibile. Di conseguenza, gradualmente i clock derivano uno rispetto l’altro. La differenza di valori tra due diversi orologi è detta clock skew.

In alcuni sistemi, ad es. nei sistemi real-time, il valore fisico del clock è importante. Da qui la necessità di capire come sincronizzare i clock fisici con gli orologi del modo reale, e come sincronizzare i clock fisici tra loro.

Quindi è necessario capire come viene misurato il tempo nel mondo reale.

Il tempo è un concetto complesso. Nel 17° secolo l’invenzione dell’orologio meccanico ha permesso la misura oggettiva del tempo, inizialmente riferendosi al tempo solare medio.

Il tempo solare medio si riferiva all’intervallo temporare che passa tra due transiti 2 consecutivi del sole: il giorno solare. Da questo derivava il secondo solare, definito come 1/86400 di un giorno solare medio.

Nel 1967/68, nell’ambito del Sistema internazionale di unità di misura (SI) il secondo è stato definito come:

«The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.» 13th CGPM (1967/68, Resolution 1; CR, 103)

«This definition refers to a caesium atom at rest at a temperature of 0 K.» (Added by CIPM in 1997)

In pratica il tempo atomico (TAI) è dato dal numero medio di transioni di vari orologi al cesio 133, misurati dal 1 gennaio 1958 e divisi per 9,192,631,770.

Con questa definizione si è resa indipendente l’unità di misura del secondo dalle misurazioni astronomiche, che dipendono da caratteristiche fisiche variabili. Ad es. perché il periodo di rotazione della Terra è in estensione, per questo attualmente il giorno calcolato con 86400 secondi TAI è più breve del giorno solare medio di 3 msec.

Lo sfasamento tra TAI e lunghezza del giorno solare medio viene risolto introducendo un intervallo di sfasamento (leap seconds) quando la differenza osservata tra le due misure supera gli 800 msec.

Questa coordinata temporale viene detta Coordinated Universal Time (UTC).

UTC tramite stazioni radio e satelliti

Esistono stazioni radio che trasmettono il tempo UTC, ad es. in USA la WWV, e in UK la MSF. Così come molti satelliti dispongono del servizio di comunicazione del tempo UTC.

Quindi è possibile utilizzare ricevitori radio ad onde corte, o da servizi satellitari, per ricevere le trasmissioni predette ottenendo un segnale UTC di riferimento. Eventualmente modificndo il segnale con il calcolo delle posizioni relative tra trasmettitore e ricevitore per correggere l’errore dovuto al ritardo della propagazione dell’onda radio.

UTC tramite GPS

Un’altra possibilità consiste nell’utilizzare il sistema GPS. Questo è un sistema distribuito di satelliti che permettono di determinare la posizione geografica di un punto della superficie terrestre.

I satelliti GPS sono posizionati ad una altitudine di 20,350 km 3. Ognuno è dotato di 4 orologi atomici, e trasmettono in continuzione la loro posizione. Ogni messaggio è marcato con il local time del satellite stesso. Ed essendo un local time ottenuto dalla media di 4 orologi atomici, è molto accurato.

Ogni device dotato di ricevitore GPS è in grado di sincronizzare con il local time dei satelliti GPS.

La localizzazione di un punto geografico sulla superficie terrestre può avvenire confrontando i segnali di tre satelliti GPS. Se si ricevono più segnali dei tre necssari, il ricevitore può calcolare le medie, ottenendo una misura più precisa del punto.

Quando si calcola la posizione tramite GPS è neessario considerare due aspetti importanti:

• la ricezione del segnale non è immediata 4;

• il clock del ricevitore in generale non è sincronizzato con quello del satellite.

Se si indica con:

• \(\Delta_r\) la deviazione (incognita) dell’orologio del ricevitore rispetto quello del satellite,

• \(T_{now}\) il tempo del ricevitore,

• \(T_{i}\) il tempo del satellite (questo è dichiarato dal satellite);

allora l’intervallo temporale per la ricezione del segnale è dato da:

\[\Delta_i = (T_{now} - T_i) - \Delta_r\]

E la distanza reale dal satellite è (c è la velocità della luce):

\[d_i = \Delta_i \cdot c = (T_{now} - T_i) \cdot c + \Delta_r \cdot c\]

Da questa si capisce che per rimuovere le incognite è necessario impostare un sistema di equazioni in cui maggiore è la quantità di satelliti, più accurato sarà il calcolo.

UTC tramite Network Time Protocol

Esistono processi che possono comunicare il tempo corrente. Server che implementano questo servizio sono detti time server.

Però anche in questo caso è necessario considerare i ritardi dovuti al processo di invio della richiesta, la sua elaborazione nel server, e per la ricezione della risposta.

È necessario effettuare una buona stima di questi ritardi. Cosa difficile, perché dipendono da fattori che sono al di fuori del nostro controllo. Il tempo di risposta della rete, dipendente dal traffico corrente. Il tempo di risposta del server, dipendente dal suo carico di lavoro. E così via.

L’algoritmo di Berkeley

Questo algoritmo si utilizza in LAN per sincronizzare gli orologi rispetto un time daemon di riferimento, usando però un algoritmo di calcolo della media dei clock delle diverse macchine coinvolte. Quindi qui lo scopo non è quello di avere una sincronizzazione con il tempo UTC.

In pratica il time daemon chiede a tutte le altre macchine i valori dei loro clock.

Queste rispondono con il delta rispetto il tempo dichiarato dal server. Il server calcola di conseguenza la variazione necessaria per allineare ogni macchina, incluso se stesso, e la comunica di conseguenza.

Ad esempio come nella seguente tabella.

computer	time	Δ	time deamon correction	correction
WS A	2:50	-10		3:05-2:50=+15
WS B	3:25	+25		3:05-3:25=-20
Time daemon	3:00	0	(-10+25+0)/3=+5 => 3:00+5 = 3:05	3:05-3:00=+05

Orologi logici

(Logical clocks) Il concetto di orologio logico è stato proposto da Leslie Lamport 5 nel 1978 (vedi [LAMP1978]) per gestire i casi in cui è necessario concordare la sequenza di eventi, senza dover per forza sincronizzare gli orologi fisici. Il precedente esempio della make ricade in questo contesto: basta sapere che out.o è stato prodotto prima della modifica di out.c.

Tra l’altro Lamport ha osservato:

• che se due processi non interagiscono, non è necessario sincronizzare i loro orologi;

• spesso non è necessario sincronizzare il valore degli orologi, ma concordare riguardo come si sono succeduti gli eventi.

Detto con maggiore enfasi: mi serve sempre il tempo? No, in alcuni casi non mi serve. L’orologio logico di Lamport non è un orologio: è un contatore di eventi.

Lamport si basa sul concetto di ordinamento parziale, e definisce una relazione happens-before, indicabile come \(a \rightarrow b\) (a happens-before b); questa significa che: avviene a, e poi avviene b.

La relazione happens-before può essere osservata direttamente:

• se a e b sono eventi che hanno luogo nello stesso processo, e a avviene prima di b, allora \(a \rightarrow b\) è vero;

• se a è l’invio di un messaggio da parte di un processo, e b è la ricezione dello stesso messaggio da parte del processo destinatario, allora \(a \rightarrow b\) è vero 6.

Per la relazione happens-before vale la relazione transitiva: \(if \: a \rightarrow b \: and \: b \rightarrow c \: then \: a \rightarrow c\).

Se due eventi a e b avvengono in processi diversi, che non si scambiano messaggi, riguardo la relazione \(a \rightarrow b\) non possiamo affermare sia vera, ma nulla possiamo affermare neanche riguardo \(b \rightarrow a\).

In un sistema complesso, formato da più macchine, utilizzando i logical clock di Lamport, e la relativa proprietà transitiva, è possibile ordinare gli eventi nell’ambito di uno stesso processo e quelli che avvengono tra processi diversi. Tutti i processi possono concordare su un tempo C(a) tale che se è vero \(a \rightarrow b\), allora è vero C(a) < C(b).

Il tempo C (Clock Time) non può essere decrescente. Le sue variazioni devono avvenire sempre sommando valori positivi, mai sottraendo.

L’implementazione dei logical clock prevede che il messaggio di sincronizzazione tra processi diversi trasporti anche il valore del logical clock della macchina che ha generato l’evento 7

Lamport ha proposto il meccanismo illustrato qui di seguito, considerando la presenza di tre diversi processi, ognuno con il suo logical clock, dotati di velocità diverse (ovvero da sx a dx incrementi di 6, di 8 e di 10).

Nel disegno a sinistra osserviamo che m1 ed m2 sono congruenti, in quanto il tempo di arrivo é superiore a quello di partenza del messaggio. Invece m3 ci pone un problema: il suo arrivo al tempo 56 non è compatibile con quello di partenza, che vale 60. Quindi il processo P2 porrà il suo orologio logico al valore di 60+1. Analogamente m4 parte a 69, ma arriverebbe a 54. Al suo arrivo il processo P1 porrà il suo orologio logico a 69+1.

L’implementazione del logical clock avviene nel middleware layer tra il livello applicativo e quello di network che trasporta il messaggio. E tipicamente:

• prima di inviare un evento, il processo P_i aggiorna il logical clock eseguendo \(C_i \leftarrow C_i + 1\);

• quando il processo P_i invia il messaggio m al processo P_j pone il timestamp di m (ts(m)) pari a C_i;

• alla ricezione di un messaggio m, il processo P_j aggiusta il suo logical clock al valore \(C_j \leftarrow max\{C_j, ts(m)\}\), quindi esegue \(C_j \leftarrow C_j + 1\) e passa il messaggio m all’applicazione.

Multicasting completamente ordinato

(Totally ordered multicasting) La necessità che i messaggi di multicasting inviati tra diversi componenti di un sistema distribuito debbano essere ordinati può essere compresa analizzando il seguente scenario.

Supponiamo di avere due processi (User1 e User2), che possono inviare comandi di modifica (Upd1 e Upd2) ai due server Replica1 e Replica2. Essendo repliche, i comandi sono inviati due volte: una per ogni server, al fine di mantenerli allineati.

Ora, supponiamo che la sequenza temporale con cui sono inviati i comandi, sia quella illustrata nella seguente figura, in cui la coordinata temporale fisica è orientata secondo le frecce orizzontali. Inoltre si ipotizza che il messaggio udp1 sia inviato ai due processo replica1 e replica2 in multicast, quindi le due «copie» partono nello stesso momento. Analogamente per il messaggio udp2.

In questo scenario, confrontando user1 rispetto user2, osserviamo che Upd1 è generato prima di upd2. Ma, mentre replica1 riceve i due comandi nell’ordine corretto, replica2 li riceve rovesciati: prima upd2 e poi upd1.

Consideriamo il fatto che upd1 può modificare un dato il cui valore viene successivamente usato da upd2. Si capisce che in questo caso l’ordine in cui arrivano i comandi è significativo, ed è necessario siano eseguiti in entrambi i sistemi con la stessa sequenza.

Quindi in alcuni casi abbiamo necessità che la sequenza di esecuzione di una serie di messaggi su più processi sia rigorosamente la stessa. Si noti che parliamo di sequenza di esecuzione, non di tempo fisico. Per questo motivo i logical clocks di Lamport sono buoni candidati per governare questo tipo di scenari.

Osservando che i logical clocks vengono regolati quando due processi interagiscono, e considerando il fatto che in un sistema formato da più processi, ogni processo interagisce con qualunque altro processo cui richiede/fornisce servizi, ne deduciamo che i logical times di tutti i processi che hanno interesse l’uno con l’altro sono mutuamente sincronizzati.

Di conseguenza la relazione di Lamport può essere utilizzata per dimostrare il concetto di totally ordered multicast, di cui abbiamo bisogno, in contesti in cui vi è un numero limitato di processi.

Qui di seguito si riporta un esempio di uso della relazione di Lamport per mostrare un ordinamento di eventi in due processi P1 e P2. La colonna del processo indica il csuo lock logico, seuito dalla colonna che indica il contenuto del messagio in uscita, quello del messaggio in entrata, la coda dei messaggi orinati secondo l’orologio logico, ed infine l’azione dell’applicazione. La prima colonna a sx è un Global clock di riscontro per il lettore: identifica la riga.

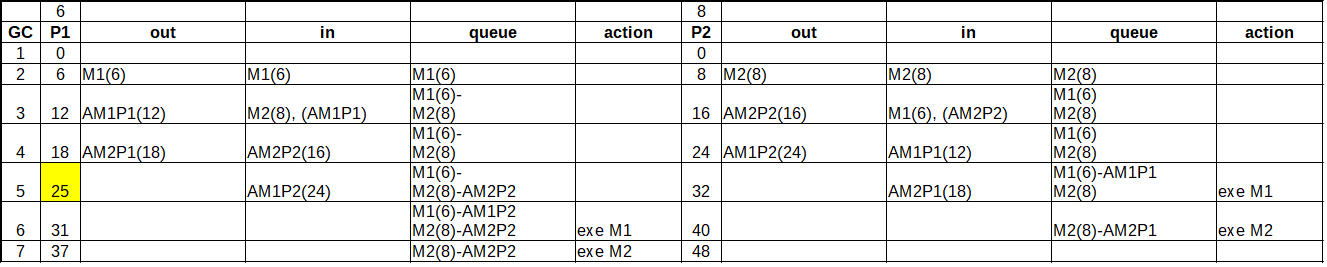
In sintesi P1 invia il messaggio di update M1 a se stesso e a P2. Mentre P2 invia il messaggio di update M2 a se stesso e a P1. Alla ricezione dei rispettivi messaggi, questi vengono messi in coda, ordinata secondo l’orologio logico: lo osserviamo alla riga 2, e alla riga 3, nelle colonne queue dei rispettivi processi.

Dopo di che le applicazioni inviano le conferme di ricezione: alla riga 3 partono AM1P1 (ack di M1, processo P1) e AM2P2 (ack di M2 processo 2) 8. Questi ack sono ricevuti alla riga 4 e al tick successivo (riga 5) sono registrati nelle code per svincolare i relativi messaggi. Questo accade per M1 in P2, in quanto è in testa alla coda, ma non ad M2 in P1; infatti M2 viene dopo M1, che P1 ancora non può eseguire perché non ha ricevuto il relativo ack da P2.

Alla riga 4 partono gli ack AM2P1 da P1 e AM1P2 da P2, che sono ricevuti alla riga 5e registrati in coda alla riga 6. Si noti che alla riga 5, i valore dell’orologio logico di P1 passa da 24 a 25, in quanto riceve un valore 24 nel timestamp di AM1P2, e per la regola di Lamport viene incrementato per non andare in conflitto.

Finalmete, alla riga 6 P1 può eseguire M1, avendo ricevuto il repatvo ack da P2, mentre P2 conclude le attività eseguendo M2 perché ha ricevuto il relativo ack da P1. All riga 7 anche P1 conclude le attività eseguendo M2.

Si osserva come entrambi i processi hanno rispettato l’ordinamento dei messaggi grazie all’uso degli orologi logici di Lamport.

Si noti che se abbiamo una rete di processi di grandi dimensioni 9, la relazione di Lamport non è più sufficiente. È necessario ricorrere ad altre soluzioni.

Conclusione

La sicronizzazione è importante nel caso di esistenza di repliche. Perché si deve assicurare che le operazioni siano esguite con lo stesso ordine nelle diverse repliche.

In questi casi i logical clock di Lamport possono essere usati per assicurare che venga rispettato l’ordine dei comandi nelle diverse repliche.

Usare l’ordine per mantenere allineate le repliche è detto State Machine Replication Approach (SMRA).

---

1

Si ricorda il comportamento del make. Un file viene trattato (compilato) se il suo sorgente ha un timestamp successivo a quello del file prodotto.

Ad esempio, nel caso di compilazione con linguaggio c, abbiamo questo processo: source-file -> object-file -> executable-file, che nell’esempio è: out.c -> out.o -> out.

Se t(out.c) > t(out.o), make lancia la compilazione di out.c per produrre un nuovo out.o.

2

Un transito solare è il momento del passaggio del sole per il suo punto più alto nell’arco della giornata.

3

la distanza di un satellite dalla Terra viene classificata in: LEO (<=2000 km), MEO ( >2000, <= 35786 km) e HEO zone (>35786 km). La frontiera MEO/HEO zones definisce l’orbita sincrona (GEO e GSO). Un satellite GSO appare fisso rispetto la superficie terrestre. I satelliti GPS sono in orbita semisincrona (SSO), ovvero completano la circumnavigazione della terra in esattamente 12 ore.

4

Servono t = s / v secondi per ricevere il segnale. Se s = 20000 km e v = 300000 km/sec, allora vale circa t = 0.0066… sec, ovvero circa 6.7 msec.

5

Computer scientist molto conosciuto. Tra l’altro, ideatore del LaTex, dei protocolli Paxos, del concetto di Bizantine Failure, e del linguaggio formale TLA+.

I protocolli Paxos servono decidere il consenso riguardo risultati ottenuti da un gruppo di processori non affidabili (ovvero, che possono fallire).

Il TLA+ (Temporal Logic of Actions) è un linguaggio formale per progettare e modellare sistemi concorrenti.

6

In quanto un messaggio non può arrivare prima di quando inviato.

7

Questo è un comportamento simile al timestamp associato ad un messaggio. Solo che, invece di far viaggiare il timestamp, viaggia il valore dell’orologio logico.

8

L’emissione quasi immediata di AM1P1 e AM2P2 è logica: sono i riscontri della ricezione dei propri messaggi di update, quindi sono generati localmente al processo dal middleware di implementazione del sistema, non c’è impegno di rete.

9

Come nel caso del calcolo di bitcoin.